Carroll's paradox

In physics, Carroll's paradox arises when considering the motion of a falling rigid rod that is specially constrained. Considered one way, the angular momentum stays constant; considered in a different way, it changes. It is named after Michael M. Carroll who first published it in 1984.

Explanation

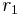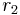Consider two concentric circles of radius r_1 and r_2 as might be drawn on the face of a wall clock. Suppose a uniform rigid heavy rod of length 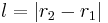l=|r_2-r_1| is somehow constrained between these two circles so that one end of the rod remains on the inner circle and the other remains on the outer circle. Motion of the rod along these circles, acting as guides, is frictionless. The rod is held in the three o'clock position so that it is horizontal, then released.

Now consider the angular momentum about the centre of the rod:

  1. After release, the rod falls. Being constrained, it must rotate as it moves. When it gets to a vertical six o'clock position, it has lost potential energy and, because the motion is frictionless, will have gained kinetic energy. It therefore possesses angular momentum.
  2. The reaction force on the rod from either circular guide is frictionless, so it must be directed along the rod; there can be no component of the reaction force perpendicular to the rod. Taking moments about the center of the rod, there can be no moment acting on the rod, so its angular momentum remains constant. Because the rod starts with zero angular momentum, it must continue to have zero angular momentum for all time.

An apparent resolution of this paradox is that the physical situation cannot occur. To maintain the rod in a radial position the circles have to exert an infinite force. In real life it would not be possible to construct guides that do not exert a significant reaction force perpendicular to the rod. Victor Namias, however, disputed that infinite forces occur, and argued that a finitely thick rod experiences torque about its center of mass even in the limit as it approaches zero width.

References